NEWTON'S LAW OF MOTION
THE LAWS OF MOTION AND
LINEAR MOMENTUM
INERTIA
Inertia is defined as the ability of a body at rest to resist
motion or a body in motion to continue moving in a straight line when abruptly
stopped.
Newton’s first law of motion
It sometimes called “the law of
Inertia”
It states that “Everybody continues
its state of rest or uniform motion in a straight line if there is no external
force acting on it”
Momentum
A body is said to be in motion if it
changes its position with time and when it has velocity
A body with zero
velocity therefore it is not in motion and hence it is at rest
The motion of a body can be measured
by multiplying out its mass ‘m’ and its velocity ‘v’ the product M.V is known
as the linear momentum of a body
Linear momentum = Mass X Velocity
= kg X m/s
= kgm/s
... The S.I unit
of momentum is kgm/s
Newton’s second law of motion
It states that the “rate of
change of linear momentum of a body is directly proportional to the applied
force and takes place in the direction of the force”
• Suppose force F acts on a body of
mass ‘m’ for time t. This force causes the velocity of the body to change from
initial velocity ‘u’ to find velocity ‘v’ in that interval t
•The change in momentum will then be
Mv – Mu (kgm/s)
•If a constant of proportionality K
is introduced in the above relation, then F = kMa. This equation can be used to
define unit of force. If m = 1kg and a = 1m/s2, then the unit of
force is chosen in such a way that when F = 1 the constant K = 1, hence F = Ma
•If a mass of 1kg is accelerating with
1m/s2, then a force 1N is said to be acting on the body. Therefore a
force F of 1N can be defined as the force which when acting on the body of mass
1kg produces an acceleration of 1m/s2, That is 1N = 1Kgm/s2
then constant of proportionality K will be equal to one.
Thus;
MASS AND WEIGHT
In the earth gravitational field,
the acceleration due to gravity is given by the symbol 'g'.
The gravitational force therefore
which act on a body of mass ‘m’ is equal to mg. This is what is known as the
weight of the body. This force tends to pull the body towards center of the
earth.
Newton’s third law of motion
•
It states that: “In every action there is an equal and opposite reaction”
EXAMPLES
1. Find the linear momentum of
a body of mass 5kg moving with the velocity of 2m/s.
Solution
Data
given
Mass = 5kg
Velocity =
2m/s
Linear momentum = mass X velocity
= 5kg X 2m/s
= 10Kgm/s
2. A football was kicked into
hands of a goal keeper at 4m/s. The goal keeper stopped the ball in 2 seconds.
If the mass of a ball is 0.5kg, calculate the average force exerted on the goal
keeper
Solution
Data given
U = 4m/s
T = 2s
Mass = 0.5kg
V = 0m/s
Solution
Data given
U = 4m/s
T = 2s
Mass = 0.5kg
V = 0m/s
F = Ma
The average force exerted by the
goal keeper is 1N
3. What force is required to
give a mass of 0.2kg an acceleration of 0.5m/s2?
Solution
Data given
Mass = 0.2kg
Acceleration (a) = 0.5m/s2
From F = acceleration X mass
F = 0.2kg X 0.5m/s2
F = 0.1N
Solution
Data given
Mass = 0.2kg
Acceleration (a) = 0.5m/s2
From F = acceleration X mass
F = 0.2kg X 0.5m/s2
F = 0.1N
4. What
acceleration will be given to a body of mass 6kg by a force of 15N?
Solution
Data given
Mass = 6kg
Force = 15N
Acceleration (a) =?
From force = mass x acceleration
Solution
Data given
Mass = 6kg
Force = 15N
Acceleration (a) =?
From force = mass x acceleration
CONSERVATION OF A LINEAR MOMENTUM
Consider the case of
firing a gun, as the bullet leaves the gun (reaction), the one holding it feels
a backward force (reaction from the butt of the gun)
According to Newton’s
third law of motion, these two forces are equal and opposite. Since these two
forces act at the same time, the impulses (i.e. change in momentum) produced
must be equal in magnitude and opposite in direction. The sum of the two
momentum is equal to zero.
This implies that momentum cannot be produced some where without producing an equal
and opposite momentum somewhere else. This is the law of conservation of linear
momentum which states that “When two or more bodies act upon each other, their
total momentum remains constant provided no external forces are acting”
Consider the collision of two balls
moving in a straight line
The balls have the masses M1
and M2 and they are approaching each other with velocity U1
and U2 fig (a)
The balls have
the velocities V1 and V2 after collision fig (b)
Let F1 and F2
be the forces acting on M1 and M2 during collision.
By Newton’s third law of
motion the forces are equal and opposite since the two forces act during the
same time t, the impulses produced are therefore equal and opposite
... F1t
= -F2t
But F1t = M1V1 – M1U1
F2t
= M2V2 – M2U2
From;
F1t = -F2t
M1V1 – M1U1
= -M2V2 + M2U2
M1V1 + M2V2
=M1U1 + M2U2
M1U1 + M2U2
= M1V1 + M2V2
This shows that the total momentum
before collision is equals to the total momentum after collision.
Question
1. A body of mass 8kg
moving with velocity of 20m/s collides with another body of mass 4kg moving
with a velocity of 10m/s in the same direction. The velocity of 8kg body is
reduced to 15m/s after collision. Calculate the final velocity of the 4kg body
Solution
Data given
Solution
Data given
M1 = 8kg
U1 =
20m/s
M2 =
4kg
U2 =
10m/s
V1
= 15m/s
V2
=?
Apply
M1U1 + M2U2
= M1V1 + M2V2
8 x20 + 4 x 10 = 8 x 15 + 4 x V2
160 + 40 = 120 + 4V2
200 = 120 + 4V2
200 – 120 = 4V2
80 = 4V2
V2 = 20m/s
... The final
velocity is 20m/s
EXERCISE
1. Define the term
momentum.
A car of
mass 500kg is moving in a straight line with a velocity of 90km/h. calculate
the linear momentum of the car
Solution
Momentum - is the product of mass and velocity
Data given
Mass = 500kg
Velocity = 90km/h
Linear momentum = mass X velocity
=
Kg X m/s
Velocity = 90km/h
Convert km into m
2.. A man of mass 80kg jumps off
a trolley of mass 160kg. If the initial speed of the man is 8m/s, at what
initial speed will the trolley move?
Solution
Data
given
Velocity =
0m/s
Mass (M1)
= 80kg
Speed (U1)
= 8m/s
Mass (M2)
= 160kg
M1U1
+ M2U2 = M1V1 + M2V2
80 X8 + 160
X U2 = 80 x 0 + 160 x 0
640 + 160U2
= 0
160U2
= 640
U2
= 4m/s
Initial
speed = 4m/s



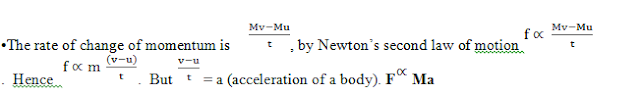













0 Comments